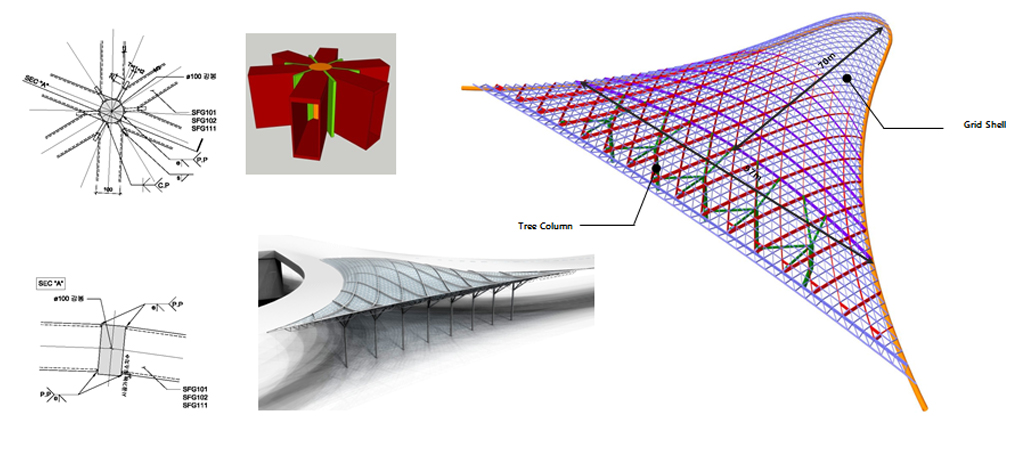
Grid shell / Lattice shell
ENGINEERING SPECIALTY
What is a grid shell?
A grid shell is a structure which derives its strength from its double curvature, but is constructed of a grid or lattice.
Grid shells are a type of spatial structure which follow the structural principles of shell action and which inherently resist the applied loads through their shape. Their fundamental characteristic is the fact that grid shells are obtained by regularly perforating the membrane of a shell and concentrating
material in the remaining strips. Thin-shell structures can be used in buildings to save materials, create an open space, or simply for the aesthetic of a smoothly curving shell. In addition to being beautiful and materials-friendly, thin-shell structures are also incredibly structurally efficient.

An optimization method for lattice shell structures under axially compressive loads is proposed aiming at the design. The method implements and improves some previous results of the fully analytical approach. The fully analytical approach provides the minimum mass solution under buckling and strength constraints, irrespective of other possible design limitations, such as, shell stiffness constraints.
Stability Analysis
Buckling is a fundamental consideration in the design and analysis of grid shells. Grid shells combine different main types of buckling.
- Member buckling: a single member buckles without acting upon the rest of the structure
- Local instability: snap-through of one or several nodes
- Global instability: the structure buckles as a whole
- A combination of the above mentioned modes
Stability results are obtained by Eigenvalue buckling analysis but also non-linear buckling analyses are performed to study the effect of imperfections on the structure.
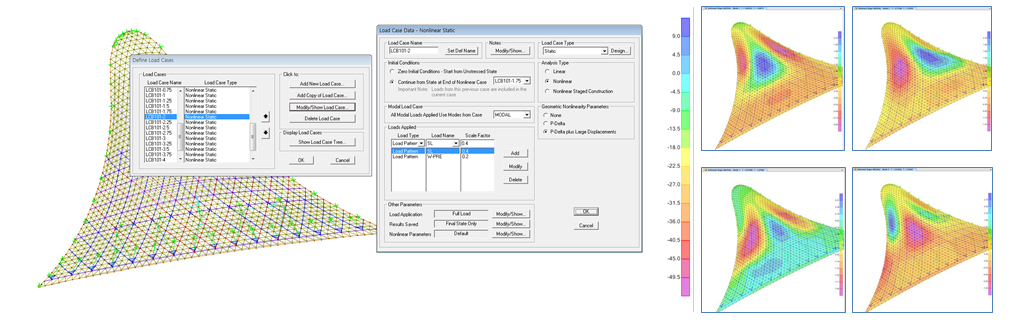
A finite element analysis is the preferred tool to analyze the buckling of grid shells. The improvement of computational power makes nonlinear analyses easier. The available computational power is such that it is now possible to couple finite element analysis with optimization methods.
The parameters involved in the analysis process are rise/span ratio, load distribution, nodal connection stiffness, and imperfection magnitude. Stability analyses are carried out to assess the buckling behavior in respect to these changing parameters and to find out:
- Influence of rise/span ratio
- Influence of load configuration (symmetrical/asymmetrical)
- Influence of nodal stiffness
- Influence of curvature radius
- Influence of imperfection magnitude on the buckling load of the shell